1 Introduction

Distributed algorithms present theoretical computer science from a different perspective.

Let’s start with an example: Imagine there is a graph with a large set of nodes - The nodes could represent anything. Maybe a network of computers exchanging information. Maybe a group of cells in a multicellular organism which exchange biochemical information continuously.

Given this graph, we might need to compute some information, let’s say we need to find a matching in this graph, or maybe we need to find a coloring of the graph that uses least number of colors (Classic graph theory problems).

Coloring problems though why? How is it useful in real-life situations? Let’s take the network of computers example. A coloring here would give a schedule to exchange information. Choose an ordering over the set of colors $C$ . Then iterate over it. At time $t$ , all the computers which are marked with color $c_{t}$ can be made active. Such a set of computers of the same color $c_{t}$ would form an independent set. Since no two nodes are neighbor in such an independent set, therefore the active computers can safely do whatever they want without disrupting the nearby computers (since they are inactive).

A general overview of computation problems that we are interested would be - Given a graph, the nodes need to work together (in the sense, exchange information) to solve some computation problem. Usually it is a graph problem - Finding a spanning tree, finding a proper vertex coloring, etc.

Distributed Problems

When we talk about distributed problems, there are few assumptions. Initially, each node is only aware of itself (For example, the color of the node itself). The final goal is such that each node knows its own part of the solution for a given computation problem (In the case of coloring, the final color the node should have). This is already enough for each node to know what to do. For example, if the node knows that its final color is $c_{t}$ , then time it should be active is time slot $t$ .

This is the key difference between sequential (classical) computing and distributed computing. In classical computer science problems, we assume that the whole input in stored in one place (For example, the complete graph), we have to process it and produce a whole output (the complete color mapping for each node in the graph).

In distributed computing, each node has no information about the whole graph, except the node itself. It knows about its neighbors and it can exchange messages only with those neighbors to explore the graph. This could be done for every node and this process could be done iteratively until every node of the graph has the complete information about the graph, but this might not be feasible in terms of communication. By communication, we mean the exchange of information between the computers. Each exchange of information could be viewed as a communication round, where each node exchanges messages with its own neighbors once. We want to minimize the number of communication rounds.

Indeed, there is an assumption here that there is some ulterior superpower/super machine that knows the whole input (i.e., the global structure of the graph), but we don’t pay much attention to this while talking about distributed problems. Also, distributed problems are differently from parallel computing problems. Parallel computing problems also have the full input/output stored at one place, except the computation is parallelized.

In other areas of computer science, we have a bird’s eye view of what the computation problem’s input looks like, while in distributed algorithms, we only have an insider’s view. We should be able to produce our own output (irrespective of other outputs) based on the information exchanged in the surroundings and so does every node should. This introduces us to the concept of locality. Fast distributed algorithms are necessarily highly localized.

By “fast” , here we talk about the number of communication rounds as well along with the classical time complexity and space complexity (computation rounds). Just how time and space are viewed as a resource, communication could also be viewed as a resource in distributed problems. This is because in general networks of computers, communication step (exchanging information) becomes the bottleneck over the computation steps. To give a perspective on how costly a communication is, getting one bit from another computer in the same local network approximately takes the same time as computing one billion arithmetic operations inside a normal computer.

Distributed algorithms heavily rely on locality. Before designing an algorithm, one should be aware of which graph problems are local and which graph problems are global. Local problems can be solved so that each node only looks at its neighbors, while global problems need the whole input graph to be available for the computation. This would also answer the question of which problems could be done using smaller number of communication rounds and which problems necessarily require larger number of rounds.

Such answers will be useful in understanding nature and fundamental limitations of any other system consisting of interacting entities such as social networks, job markets etc.

Coloring Cycles Fast

Let’s look at a very fast distributed algorithm. We will have a simple setting - A graph which is a directed cycle. Each node has exactly one successor and one predecessor. Let’s say we need a proper $k$ -coloring i.e., each node has to be labelled with a label varying from $0$ to $k - 1$ and labels of any pair of neighbors are always different.

We’ll assume that initially the nodes are already colored with some color. This is a valid assumption in a real life setting, because each computer could be mapped to a unique identifier from a large set of identifiers. Think of this like an IP address. Currently, the number of colors is as large as the maximum value of any computer’s identifier, we would like to reduce the number of colors.

Let’s say we already have a coloring with 256 numbers (labels from $0$ to $255$ ).

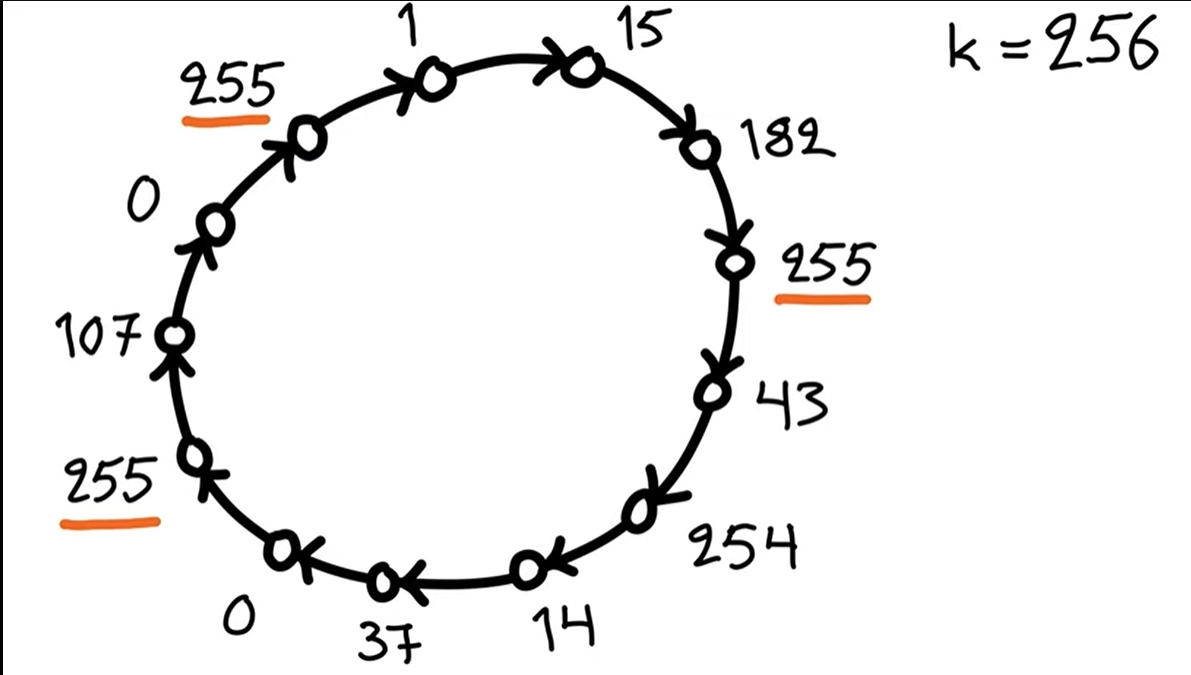
One algorithm would be to follow a simple strategy: In each step, a node is active if it is a local maximum. The active nodes will then pick a color which is free from the color that the neighbors already have. This process is continued until all the nodes stop changing their colors. It can be shown that we can reduce any number of coloring to a 3-coloring since each node has at most two neighbors in the graph.

Let’s write this algorithm as a pseudocode, we should keep in mind that all the nodes in the network run the same algorithm. Let $c$ be the unique identifier of the the node. Pseudocode is given as follows.

while(true){
	Send message c to all neighbors
	Receive messages from all neighbors. Let M be the set of messages received
	If c != 1 && c != 2 && c != 3 && c > max(M){
		c = min({1 , 2 , 3} \ M) 
	}
}

Let’s call $c = 1, 2, 3$ as stopping state. Once a computer reaches a stopping state, it never changes it state, meaning eventually all the computers would reach this state and the process will end at some finite time. We can rewrite the algorithm without while(true) by breaking out of the loop whenever the node reaches the stopping state.

Faster coloring with Unique identifiers

In worst case, the algorithm above is not particularly efficient. For example, if we had a chain/cycle with increasing node values, in each round at most two nodes reach the stopping state, which means that it takes $Θ (n)$ rounds until all nodes have stopped. But we can do much faster. For $n = 256$ unique identifiers initially, in one round, we can reduce the number of colors to $16$ .

We can represent the unique identifiers in terms of binary. For example, let’s take a node $a$ with value

v_{a} = (123)_{10} = (01111011)_{2}

whose successor node $a^{'}$ (marked with a prime) has values

v_{a^{'}} = (47)_{10} = (00101111)_{2}

Consider the index of the lowest bit that differs i.e.,

v_{a} [i] \neq = v_{a^{'}} [i]

Now let the index be $i$ in binary and the value of $v_{a} [i]$ be $j$ , where $j$ is $0$ or $1$ . Define the new color of node $a$ as concatenation of $i$ and $j$ . In other words, set

v_{a} = 2 \cdot i + j

Note that $i$ is at most 3 digits and $j$ is a single bit, thus this new color’s value is less than $16$ . This process is done by all the nodes in a single round.

Note that this always produces a proper coloring. To see this, consider a pair of nodes $a$ and $b$ so that $b$ is the successor of $a$ . By definition, $v_{a^{'}} = v_{b}$ , we need to show that $v_{a} \neq = v_{b}$ . If the indices in which $a$ differs from $a^{'}$ is same as $b$ differs from $b^{'}$ , then $j$ cannot be same for both as it would imply that $a$ doesn’t differ from $a^{'}$ in that index which is contradiction. If the indices in which those two differ are different, then $v_{a}$ can never be equal to $v_{b}$ since one of them will be at least be greater than the other by one regardless of what $j$ is chosen for both the nodes.

The algorithm reduces $2^{x}$ colors to $2 x$ colors in one round. If we iterate the algorithm, we can reduce the number of colors $n$ to $6$ in $O (log^{*} x)$ rounds. Once we have reduced it to $6$ colors, we can then reduce it to $3$ colors by the algorithm we discussed previously in $3$ rounds.

Coloring with Randomized Algorithms

Here is a fairly straightforward algorithm. Each node has a flag $u_{a} \in {0, 1}$ , indicating whether it has stopped or not, and value $v_{a}$ . Once $u_{a}$ is $1$ , the node outputs $v_{a}$ .

In each step, every node with its flag set to $0$ , picks a new color $c$ from ${1, 2, 3}$ uniformly at random. Then each node sends it current color to its neighbor. If $c$ is different from that of its neighbors, then the flag is set to $1$ and the node stops. Otherwise this continues.

It is easy to see that in each step, a node $a$ will stop with probability $1/3$ . Fix a positive constant $C$ . Let

k = (C + 1) log_{3/2} n

where $n$ is the number of nodes in the graph. Now if we run this algorithm for $k$ steps, the probability that a given node $a$ has not stopped is

(\frac{2}{3})^{k} = (\frac{1}{n})^{C + 1}

By the union bound, the probability that there is a node that has not stopped is at most

p = \frac{1}{n ^{C}}

Thus, with probability at least $1 - p$ , all nodes have stopped after $k$ steps. For any given constant $C$ , there is an algorithm that runs for $k$ = $O (log n)$ rounds and produces a proper 3-coloring of a path with probability $1 - \frac{1}{n ^{C}}$ .

Exercises

Will be added soon

Indefinite Tree

Explorer