2 Graph Theoretic Foundations

---

Basic Terminologies such as

• Undirected and directed graphs
• Adjacency , Degree , k-regular
• Subgraphs , Induced subgraph (Vertex/Edge induced) , Spanning subgraph
• Walks, Cycles, Paths, Trail
• Connectivity, Distance, Diameter, Tree, Isomorphism

are assumed to be known already.

---

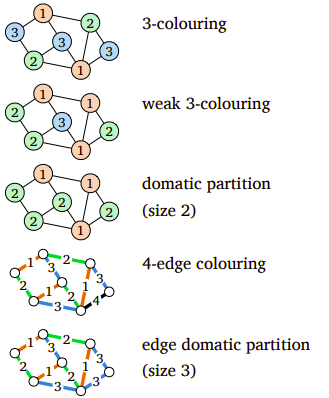
Packing and Covering

A subset of nodes $X\subseteq V$ is

• an independent set if each edge has at most one endpoint in $X$ . In other words, $|e\cap X|\le 1$ for all $e\in E$ .
• a vertex cover if each edge has at least one endpoint in $X$ . In other words, $e\cap X\ne \varnothing$ for all $e\in E$ .
• a dominating set if each node $v\notin X$ has at least one neighbor in $X$. In other words, ${\mathrm{ball}}_G(v,1)\cap X\ne \varnothing$ for all $v\in V$, where

$${\mathrm{ball}}_G(v,r)=\{u\in V:{\mathrm{dist}}_G(u,v)\le r\}$$

A subset of edges $X\subseteq E$ is

• a matching if each node has at most one incident edge in $X$. In other words, $\{t,u\}\in X\&\{t,v\}\in X⟹u=v$ .
• an edge cover if each node has at least one incident edge in $X$ . In other words, ${\bigcup }_{i\in u,v}X=V$ .
• an edge dominating set if each edge $e\notin X$ has at least one neighbor in $X$. In other words, $e\cap \left(\bigcup X\right)\ne \varnothing$ for all $e\in E$.

Labelings and Partitions

We will often encounter functions of the form

$$f:V\to \{1,2,...,k\}$$

There are two interpretations that are often helpful:

• Function $f$ assigns a label $f(v)$ to each node $v\in V$.
• Function $f$ is a partition of $V$. More specifically, $V=V_1\cup V_2\cup ...\cup V_k$ where $V_i=f^{-1}(i)=\{v\in V:f(v)=i\}$ .

Similarly, we can have functions of the form

$$f:E\to \{1,2,...,k\}$$

and interpret it as a labeling of edges or as a partition of $E$ .

We say that a function $f:V\to \{1,2,..,k\}$ is

• a proper vertex coloring if $f^{-1}(i)$ is an independent set for each $i$ .
• a weak coloring if each non-isolated node $u$ has a neighbor $v$ with $f(u)=f(v)$ .
• a domatic partition if $f^{-1}(i)$ is a dominating set for each $i$.

A function $f:E\to \{1,2,...,k\}$ is

• a proper edge coloring if $f^{-1}(i)$ is a matching for each $i$
• an edge domatic partition if $f^{-1}(i)$ is an edge dominating set for each $i$.

Factors and Factorizations

Let $G=(V,E)$ be a graph, let $X\subseteq E$ be a set of edges, and let $H=(U,X)$ be the subgraph of $G$ induced by $X$ . We say that $X$ is a $d$-factor of $G$ if $U=V$ and ${\mathrm{deg}}_H(v)=d$ for each $v\in V$ .

Equivalently, $X$ is a $d$-factor if $X$ induces a spanning $d$-regular subgraph of $G$. A function $f:E\to \{1,2,...,k\}$ is a $d$-factorization of $G$ if $f^{-1}(i)$ is a $d$-factor for each $i$ .

Following observations can be made from this

• A $1$-factor is a maximum matching. A $1$-factorization is an edge coloring.
• The subgraph induced by a $2$-factor consists of disjoint cycles.
• A $1$-factor is also known as perfect matching.

Approximations

Formally, the definition of a maximization problem consists of two parts: a set of feasible solutions $F$ and an objective function $g:F\to \mathbb{R}$ . In a maximization problem, the goal is to find a feasible solution $X\in F$ that maximizes $g(X)$. A minimization problem is analogous.

Often it is infeasible or impossible to find an optimal solution, hence we resort to approximations. Given a maximization problem $(F,g)$, we say that a solution $X$ is an $\alpha$-approximation if $X\in F$, and we have $\alpha \cdot g(X)\ge g(Y)$ for all $Y\in F$ . Note that $\alpha \ge 1$ in this case. The same applies for a minimization problem as well, with the constant on the other side with reverted inequality.

---

Let’s prove a example theorem.

Claim:

In any $d$-regular graph $(d\ge 1)$, a minimum vertex cover is always a $d$-approximation of a minimum dominating set.

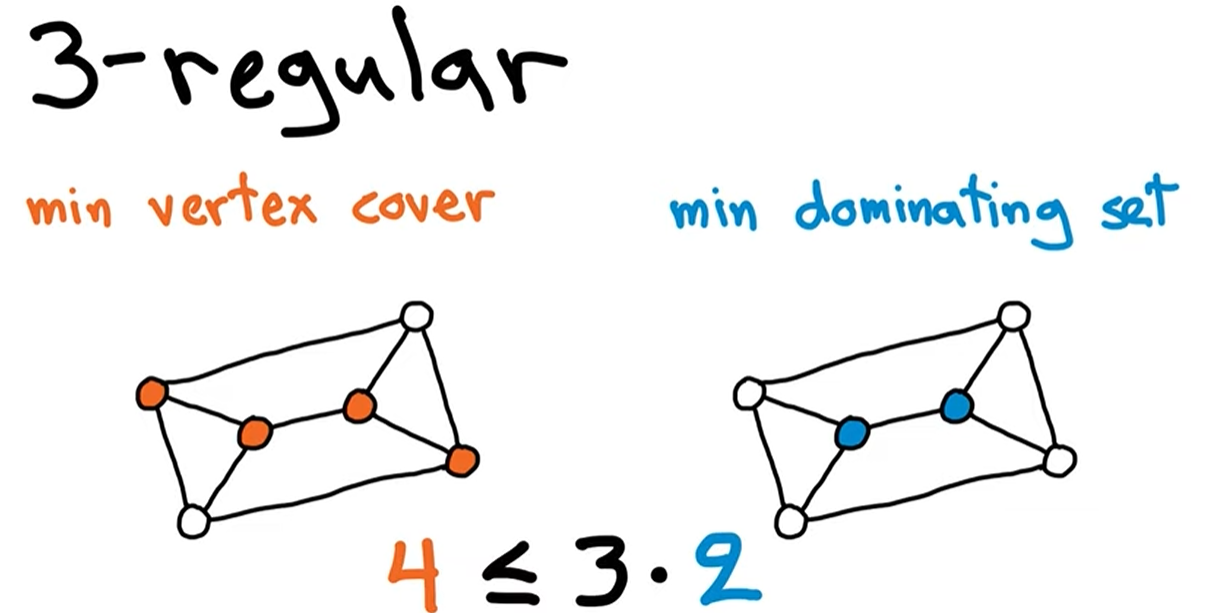
Proof:

First let us a show that a minimum vertex cover is a dominating set. Let $X$ be any vertex cover. It is fairly straightforward that since $X$ is a vertex cover, every edge has at least one endpoint in $X$, which means any node $u$ which is not in $X$ has at least one of its neighbor in $X$.

Now to show that the minimum vertex cover is always a $d$-approximation of a minimum dominating set, consider a minimum vertex cover $X^{\prime }$ and a dominating set $Y$. We need to show that $|X^{\prime }|\le d\cdot |Y|$ .

Since the graph is $d$-regular, therefore $(d+1)\cdot |Y|\ge |V|$ . This is because for any vertex in $Y$ , since it has a degree $d$ and by the definition of dominating set, the union of neighbors ($d$ neighbors) and vertex itself from all the vertices in $Y$ must contain all the vertices in the graph.

Consider $A=V\setminus X^{\prime }$ , the set of nodes that are not in the minimum vertex cover $X^{\prime }$.

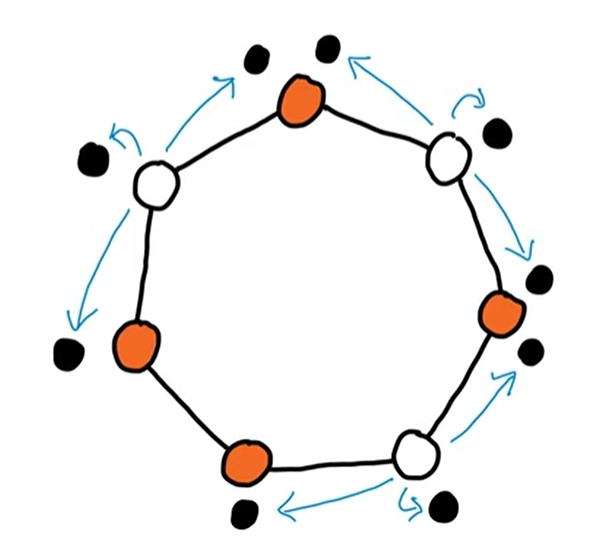
Similar to the above argument, $(d+1)\cdot |A|\ge |V|$ . Again to put in perspective, this says that the union of all neighbors and vertex itself for each vertex in $A$ equals $V$. This is not really evident at first. Let’s prove this by contradiction. Suppose there was a vertex $u$ such that it is missed out while taking the union. Now $u\notin A$ and all the neighbors of $u$ are also not in $A$. This means that $u$ and all the neighbors of $u$ both belong to the set $X^{\prime }$ . But this leads to a contradiction, since removing $u$ from this set still gives us a vertex cover which has a cardinality lesser than $X^{\prime }$.

The result now follows up eventually. We know

$$\begin{array}{r}|A|\ge \frac{|V|}{d+1}\end{array}$$

Since $|X^{\prime }|=|V|-|A|$ , therefore

$$\begin{array}{r}|X^{\prime }|\le \frac{d}{d+1}|V|\end{array}$$

Previously, we had $|V|\le (d+1)\cdot |Y|$ . Combining these two, we get

$$\begin{array}{r}|X^{\prime }|\le d\cdot |Y|\end{array}$$

which is the required result.

One key point to note is that we didn’t really use the property that $X^{\prime }$ is a minimum vertex cover, rather we used the property that any minimum vertex cover is also a minimal vertex cover. Thus, this claim holds true even when we consider any minimal vertex cover.

What if we used any vertex cover instead of $X^{\prime }$ ? The statement doesn’t hold true now. The simplest counterexample would be considering the vertex cover that covers all the vertices. Choose $|V|=4$ and $d=3$. Here $|Y|=1$ , while $|X|=4$, contradicting the claim.

---

Exercises

Will be added soon